Sample experiment using Sliding Window Regression

Introduction

SlidingWindowReg implements a regression model for hydrological time series data. In particular, multiple time-lagged windows with Gaussian kernel shape are estimated from training data. Then, each extracted feature is mapped to a target time series via multiple linear regression.

In this vignette, a sample experiment is performed to demonstrate that the model is able to identify model parameters correctly in a user-simulated setup.

Data preparation & experimental setup

First, we load the package and the sample watershed data:

library(SlidingWindowReg)

data("sampleWatershed")

As a second step, we divide the dataset into (a) a train set containing 30 years (77% of the time series) and (b) a test set comprising the residual 9 years (23% of the time series). Note that in the present dataset, years refer to hydrological years (October 01 to September 30).

library(lubridate) # package to handle date formats

## 
## Attaching package: 'lubridate'

## The following objects are masked from 'package:base':
## 
##     date, intersect, setdiff, union

hydr_year <- cumsum(format(sampleWatershed$date, "%d.%m.") == "01.10.") # determine hydrological years (Oct 01 to Sep 30)

train_inds <- which(hydr_year <= 30)

SlidingWindowReg model

Given the data splits, we train the SlidingWindowReg model on the train set. For this purpose, the following parameters are set:

iter number of iterations (maximum number of windows)
runs number of independent model runs — by default, the run achieving the best performance metric is returned
param_selection method to determine the number of windows

Model training

In the presented example, we use 3 iterations (up to 3 windows), and determine the hyperparameter (number of windows \(k\)) with respect to the Bayesian Information Criterion (BIC).% Further, we set the parallelization procedure to FALSE.

mod <- trainSWR(sampleWatershed$rain[train_inds],
                sampleWatershed$gauge[train_inds],
                iter = 3,
                param_selection = "best_bic")

## Warning: The `runs` argument of `trainSWR()` is deprecated as of SlidingWindowReg 0.1.1.
## ℹ Multiple model runs are not useful with deterministic window initializations.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

## Warning: The `parallel` argument of `trainSWR()` is deprecated as of SlidingWindowReg
## 0.1.1.
## ℹ Parallel model runs are not useful with deterministic window initializations.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

## Warning: The `return` argument of `trainSWR()` is deprecated as of SlidingWindowReg
## 0.1.1.
## ℹ Return argument is unused.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.

The optimizer GENOUD (Genetic optimization using derivatives) is used by default. Alternatively, the package supports derivative-free optimization as well: the algorithm argument can be set to algorithm = “BOBYQA”.

mod_BOBYQA <- trainSWR(sampleWatershed$rain[train_inds],
                sampleWatershed$gauge[train_inds],
                iter = 3,
                param_selection = "best_bic",
                algorithm = "BOBYQA")

%## Parallelization

%Model parallelization is implemented between the model runs, while iterations (incrementally adding windows in each iterations) run in a %serial order. Hence, the option parallel = FALSE should be chosen if runs = 1. In case of multiple model runs, %parallel can be set to either TRUE (in this case, the number of available kernels is determined automatically), or to a %positive integer number indicating the number of kernels to be used.

Evaluation

Tools for evaluating the model results include summary and plot functions for the model parameters, as well as metrics and plots to determine the predictive performance on test sets.

Model parameters

A first overview on the model results can be obtained by printing a model summary:

summary(mod)

## SlidingWindowReg (SWR) model object with k = 2 windows
## 
## | window| delta| sigma| beta|
## |------:|-----:|-----:|----:|
## |      1|  0.17|  6.28| 0.41|
## |      2|  1.28|  0.22| 0.47|

In specific, the main model parameters are stored as:

a matrix characterizing the location and size of the windows (column 1 indicates all center points on the time axis, column 2 indicates the variance)
a vector of regression coefficients

# window parameters
print(mod$param)

##          delta     sigma
## [1,] 0.1666667 6.2787582
## [2,] 1.2816116 0.2221428

# regression parameters
print(mod$mix)

## [1] 0.4089494 0.4650226

In order to visualize the estimated windows, a kernel plot is available in SlidingWindowReg:

coef(mod)

##                  -20          -19          -18         -17         -16
## kernel1 0.0003298943 0.0005381571 0.0008559532 0.001327387 0.002007022
## kernel2 0.0000000000 0.0000000000 0.0000000000 0.000000000 0.000000000
##                 -15        -14         -13         -12       -11        -10
## kernel1 0.002958784 0.00425286 0.005960131 0.008143992 0.0108499 0.01409357
## kernel2 0.000000000 0.00000000 0.000000000 0.000000000 0.0000000 0.00000000
##                 -9         -8         -7        -6         -5         -4
## kernel1 0.01784938 0.02204104 0.02653676 0.0311509 0.03565335 0.03978661
## kernel2 0.00000000 0.00000000 0.00000000 0.0000000 0.00000000 0.00000000
##                   -3         -2         -1           0
## kernel1 4.328929e-02 0.04592308 0.04749943 0.047901900
## kernel2 9.629576e-09 0.07569607 0.38922563 0.000100905

plot(mod, include_text = FALSE)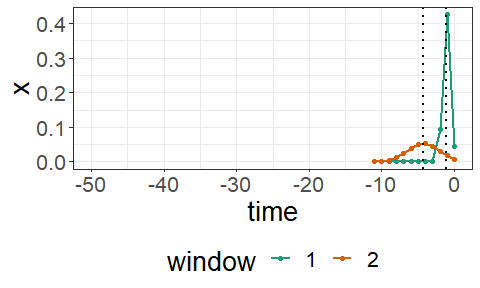

Predictive performance

To assess its predictive performance, we evaluate the model on the test set. For this purpose, we compute the root mean squared error (RMSE) and further evaluation metrics:

pred_on_test <- predict(mod, 
                        newdata = sampleWatershed$rain[-train_inds])

print(eval_all(pred_on_test, 
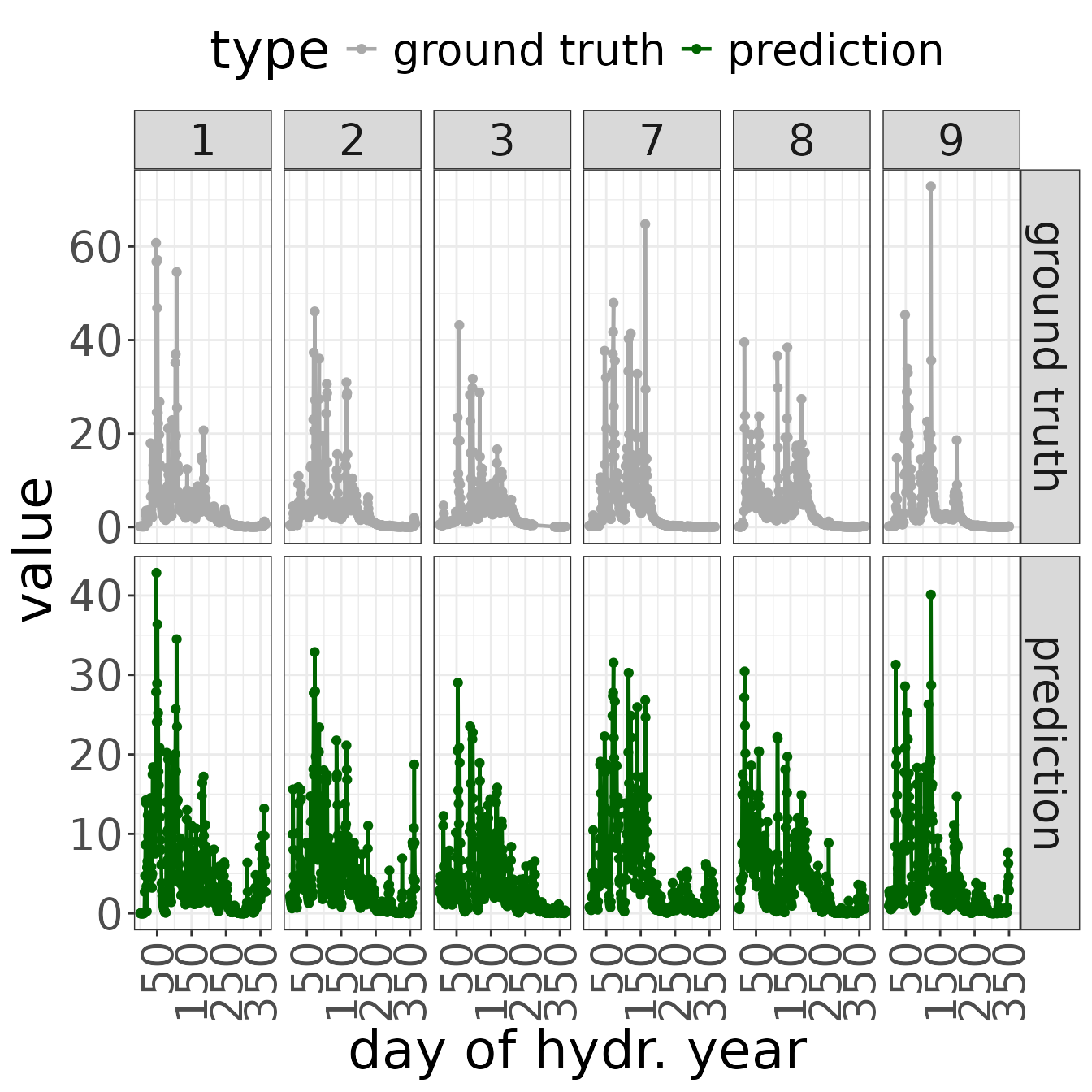
               sampleWatershed$gauge[-train_inds]))

##      rmse     nrmse        r2       nse       kge
## 1 3.34196 0.8868558 0.7263176 0.7263176 0.7500152

As a next step, we generate a plot demonstrating

the input time series,
the predicted output time series, and
the ground truth output.

The plot demonstrates the first 3 and last 3 hydrological years (in this case, years 1-3 and 7-9 are displayed).

plot(mod, 
     type = "prediction",
     reference = sampleWatershed$gauge[-train_inds],
     newdata = sampleWatershed$rain[-train_inds])

Stefan Schrunner